后门准则

本次分享的知识来源于《Causal Inference in Statistics：A Primer》的翻译版本《统计因果推理入门》，该书由杨娇云等人翻译，主要包括因果学习的基础知识。
电子图书获取方法：
关注公众号“AI八倍镜”并回复“因果学习”。

知识回顾

在上一小节“校正公式”当中，学习到：

1. 在固定X取值x的情况：用do(x)表示。
2. P( Y=y | do( X=x ) ) 表示通过干预使得X=x时 Y=y的概率，反映了如果群体中的每个个体均将X值固定为x时，Y的总体分布。
3. P(Y=y | do(X=x), Z=z) 表示对于给定的Z=z，干预do(X=x)得到的分布中Y=y的条件概率。

最后的结论是：确定一个变量对另一个变量的因果效应时，需要讲该变量的父节点变量进行校正。

问题

在现实生活中的问题中，变量通常有不可观察的父节点，那么如何从观察到的非干预数据集中计算变量间的因果效应？对于因果图结构而言，如何利用因果图结构计算数据的因果效应？

解决

基于上述问题，引入了后门准则。首先，介绍一种新的名词叫后门路径：
如果一条连接X和Y的路径中，有指向X的箭头，则这条路径被称为从X到Y的后门路径。

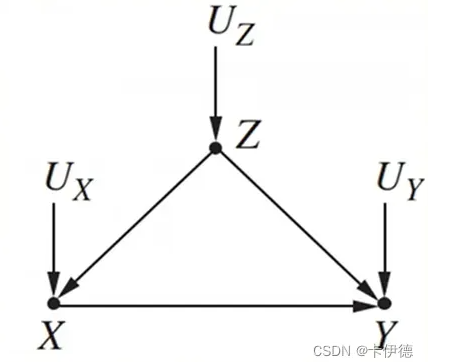
例如，对上图来说，X←Z→Y就是一条后门路径。

那么，后门准则的定义为：给定有向无环图中的一对有序变量（X，Y），如果变量集合Z满足：

（1）Z中没有X的后代节点；
（2）Z阻断了X与Y之间的每条含有指向X的路径；

则称Z满足关于（X，Y）的后门准则。

若变量集合Z满足（X，Y）的后门准则，则X对Y的因果效应公式：

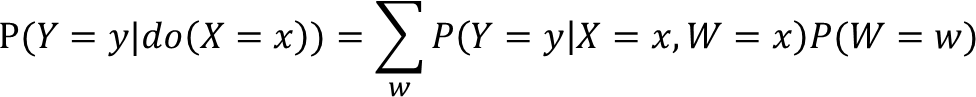
一般来说，后门准则中的节点集合Z满足下列条件：

1)阻断X和Y之间每条含有指向X的路径; (Z在后门路径中)
2)保持所有从X到Y的有向路径不变; (Z不为X的任何后代节点)
3)不会产生新的含有指向X的路径。(Z不为任何对撞节点)

后门准则的应用场合是：

变量通常有不可观察的父节点，节点值无法得到，需要一个替代的变量集合用于校正。后门准则可以确定，对于由有向无环图表示的因果模型中的任何两个变量X和Y，应该以模型中的哪些变量Z为条件来寻找X和Y之间的因果关系。

例子

例如，对上图所示的因果图来说，试图获取 药物X 对痊愈率Y 的因果效应，测量了体重W（影响痊愈率），加入了经济社会地位Z（影响患者体重和对接受质量的选择，缺失统计数据）。

那么就可以以节点W作为条件：

（1）阻断了X←Z→W→Y路径；
（2）非X的后代；

则，X对Y的因果效应公式可表示为：

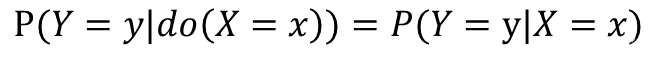
拓展

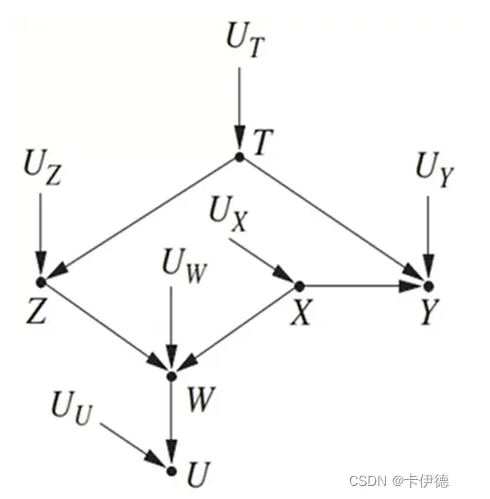
对于上图来说，不存在X到Y的后门路径，即空集满足后门准则，则不需要校正，校正公式：
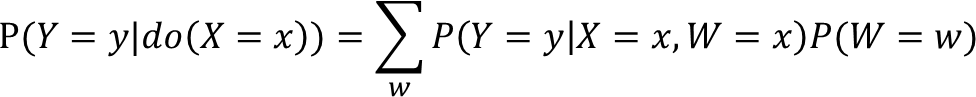此外，如果固定W为w，则产生新的伪路径：X→Z←T→Y，选择以T为条件阻断X→Z←T→Y ，校正公式：
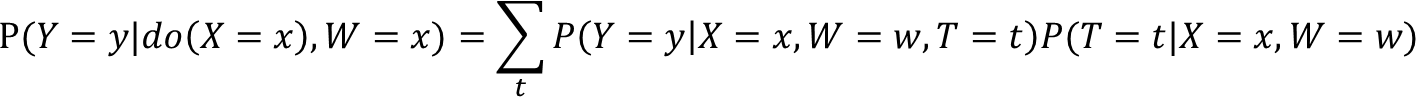上式称为W-特定因果效应，后续章节还会用到该效应。

电子图书获取方法：
关注公众号“AI八倍镜”并回复“因果学习”。

前面的知识后后面的知识还会继续更新和补充，请持续关注~